Old Music Theory

For the following harmonic formula:

to be reduced to three parts, one of the parts should be suppressed preferably.

Its obvious that suppressing the intermediate part holding the G will do less harm to the realization of the harmony than suppressing any other part. Example:

This way the root is suppressed, on three different occasions on the 5th degree chord, without destroying its tonal effect. In the harmonic relationship of the two notes B and D, no ear will hear the 7th degree instead the 5th.

In the following example:

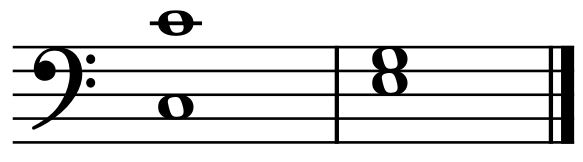
The two notes E and G don’t produce the effect of the 3rd degree (E, G, B), it produces the effect of the 1st degree with a suppressed root.

From this, we can conclude the following:

1. Every incomplete chord whose notes belong to two or more different degrees, is always heard by the ear as the best possible degree or the most used. In this case, the musical sense always fills in the suppressed note.
2. Its not necessary to constantly complete all the chords in harmony. Also, the suppression of certain notes allow for various effects. Aside from musical interest, the ease of melodious singing of each part should be prioritized. Therefore, the suppression of the notes of a chord must be motivated by the melodic interest of the parts, even if the number of parts allow all notes of a chord to be played.